The proof presented below, giving an (almost) complete characterisation of constructible regular polygons, is such a beautiful gem of a proof that I can’t help but record it here so that I might not forget it. I’ll go over far more details than is usually done, simply because it amuses me how many different areas of undergraduate mathematics are touched upon.
Theorem 1 The regular  -gon is constructible by ruler and compass if and only if
-gon is constructible by ruler and compass if and only if  has the form
has the form 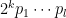 , where
, where 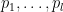 are distinct primes of the form
are distinct primes of the form 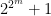 .
.
Primes of this form are called Fermat primes. The only known Fermat primes are 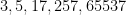 , and heuristics suggest that there may be no others, though this is an open problem.
, and heuristics suggest that there may be no others, though this is an open problem.
We must say what we mean by “constructible”. We assume we are given a plane (a sheet of paper, say), with two points already labelled. We parameterise the plane by points of  , and we rotate and scale so that the two labelled points are
, and we rotate and scale so that the two labelled points are  and
and  . There are three things we are allowed to do:
. There are three things we are allowed to do:
- Whenever we have two labelled points we can draw the straight line through them.
- Whenever we have two labelled points we can draw the circle with one as centre and the other on the circumference.
- We can label any point of intersection (of two lines, two circles, or a line and a circle).
Any point of the plane (considered as an element of  ) that can be labelled through a sequence of the above operations is called constructible. Denote by
) that can be labelled through a sequence of the above operations is called constructible. Denote by  the set of constructible numbers.
the set of constructible numbers.
Lemma 2 The set  is the smallest subfield of
is the smallest subfield of  closed under taking square roots.
closed under taking square roots.
The lemma can be proved as follows.
- Show closure under
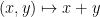 by constructing the parallelogram with vertices
by constructing the parallelogram with vertices  .
.
- Show closure under the rotation
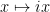 .
.
- Show closure under taking real parts. Hence
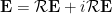 , where
, where 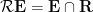 .
.
- Show closure under
 for
for  by constructing the right triangle with leg lengths
by constructing the right triangle with leg lengths 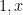 and the similar right triangle with base
and the similar right triangle with base 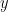 . Deduce that
. Deduce that  is a ring.
is a ring.
- Show that if
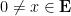 then
then 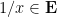 by doing so first for
by doing so first for 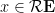 (another right triangle construction) and then using
(another right triangle construction) and then using 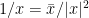 . Thus
. Thus  is a field.
is a field.
- Show that
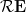 is closed under taking square roots (yet another right triangle construction). Thus show that
is closed under taking square roots (yet another right triangle construction). Thus show that  is closed under taking square roots by bisecting an appropriate angle.
is closed under taking square roots by bisecting an appropriate angle.
- Finally show that any subfield
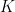 of
of  closed under taking square roots is closed under the “constructing” rules we listed when defining
closed under taking square roots is closed under the “constructing” rules we listed when defining  . The idea here is that one never has to solve an equation worse than a quadratic (when intersecting two circles, first construct the perpendicular bisector to the segment connecting the two centres, and then compute the intersection of this line with one of the circles).
. The idea here is that one never has to solve an equation worse than a quadratic (when intersecting two circles, first construct the perpendicular bisector to the segment connecting the two centres, and then compute the intersection of this line with one of the circles).
The following is our algebraic characterisation of constructibility.
Lemma 3 We have 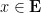 if and only if the degree
if and only if the degree ![{[K:\mathbf{Q}]}](https://s0.wp.com/latex.php?latex=%7B%5BK%3A%5Cmathbf%7BQ%7D%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) of the normal closure
of the normal closure 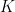 of
of  is a power of
is a power of  .
.
Proof: By the previous lemma,  can be described as the union of all fields
can be described as the union of all fields 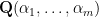 such that
such that  for all
for all 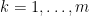 . Let
. Let 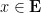 . Thus
. Thus  lies in some such field
lies in some such field 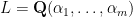 . But note by the tower law that
. But note by the tower law that
![\displaystyle [L:\mathbf{Q}] = \prod_{k=1}^{m} [\mathbf{Q}(\alpha_1,\ldots,\alpha_k):\mathbf{Q}(\alpha_1,\ldots,\alpha_{k-1})],](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5BL%3A%5Cmathbf%7BQ%7D%5D+%3D+%5Cprod_%7Bk%3D1%7D%5E%7Bm%7D%C2%A0%5B%5Cmathbf%7BQ%7D%28%5Calpha_1%2C%5Cldots%2C%5Calpha_k%29%3A%5Cmathbf%7BQ%7D%28%5Calpha_1%2C%5Cldots%2C%5Calpha_%7Bk-1%7D%29%5D%2C&bg=ffffff&fg=000000&s=0&c=20201002)
where each factor ![{[\mathbf{Q}(\alpha_1,\ldots,\alpha_k):\mathbf{Q}(\alpha_1,\ldots,\alpha_{k-1})]\leq 2}](https://s0.wp.com/latex.php?latex=%7B%5B%5Cmathbf%7BQ%7D%28%5Calpha_1%2C%5Cldots%2C%5Calpha_k%29%3A%5Cmathbf%7BQ%7D%28%5Calpha_1%2C%5Cldots%2C%5Calpha_%7Bk-1%7D%29%5D%5Cleq+2%7D&bg=ffffff&fg=000000&s=0&c=20201002) . Thus
. Thus ![{[L:\mathbf{Q}]}](https://s0.wp.com/latex.php?latex=%7B%5BL%3A%5Cmathbf%7BQ%7D%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) is a power
is a power  , and by another application of the tower law so is
, and by another application of the tower law so is ![{[K:\mathbf{Q}]}](https://s0.wp.com/latex.php?latex=%7B%5BK%3A%5Cmathbf%7BQ%7D%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) .
. 
Conversely suppose that ![{[K:\mathbf{Q}]}](https://s0.wp.com/latex.php?latex=%7B%5BK%3A%5Cmathbf%7BQ%7D%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) is a power of
is a power of  . Then the Galois group
. Then the Galois group 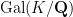 is a
is a  -group. Recall that any
-group. Recall that any  -group
-group  (except the trivial group) has nontrivial centre: by counting conjugacy class sizes, the size of
(except the trivial group) has nontrivial centre: by counting conjugacy class sizes, the size of 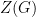 must be divisible by
must be divisible by  . Thus by induction (and classifying abelian
. Thus by induction (and classifying abelian  -groups) it follows that in every
-groups) it follows that in every  -group
-group  there is a sequence of normal subgroups
there is a sequence of normal subgroups 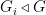 such that
such that 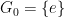 ,
,  , and
, and 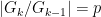 for each
for each  . Specialising to
. Specialising to 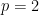 , Galois theory now implies that
, Galois theory now implies that 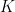 is the top of a tower of quadratic extensions starting from
is the top of a tower of quadratic extensions starting from  , so
, so 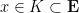 .
.
By saying “the  -gon is constructible” we mean that the vertices of some regular
-gon is constructible” we mean that the vertices of some regular  -gon are constructible. Clearly this is equivalent to saying
-gon are constructible. Clearly this is equivalent to saying  is an element of
is an element of  . Note that
. Note that  , where the
, where the  th cyclotomic polynomial
th cyclotomic polynomial 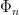 is defined by
is defined by
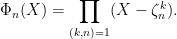
Note that ![{\prod_{d|n} \Phi_d(X) = X^n-1 \in \mathbf{Z}[X]}](https://s0.wp.com/latex.php?latex=%7B%5Cprod_%7Bd%7Cn%7D+%5CPhi_d%28X%29+%3D+X%5En-1+%5Cin+%5Cmathbf%7BZ%7D%5BX%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) , so by the uniqueness of polynomial division and induction we have that
, so by the uniqueness of polynomial division and induction we have that ![{\Phi_n(X) \in \mathbf{Z}[X]}](https://s0.wp.com/latex.php?latex=%7B%5CPhi_n%28X%29+%5Cin+%5Cmathbf%7BZ%7D%5BX%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) .
.
Lemma 4 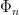 is irreducible over
is irreducible over  .
.
Proof: Suppose  where
where  is irreducible and
is irreducible and  . We must show that each
. We must show that each 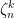 is a root of
is a root of  . Since some
. Since some 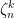 is a root of
is a root of  , it suffices to show that
, it suffices to show that  implies
implies  whenever
whenever  is a prime not dividing
is a prime not dividing  . Towards this end, suppose that
. Towards this end, suppose that  is such a prime and
is such a prime and  but
but 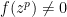 . Then
. Then 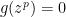 since
since 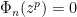 . Since
. Since  is irreducible this implies that
is irreducible this implies that  divides
divides 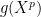 . Denoting reductions modulo
. Denoting reductions modulo  by a tilde and using Freshman’s dream,
by a tilde and using Freshman’s dream,  divides
divides 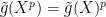 . Thus
. Thus  and
and  are not coprime, so
are not coprime, so 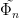 , and thus
, and thus  , has a multiple root over
, has a multiple root over  . But this is a contradiction since
. But this is a contradiction since  and its formal derivative
and its formal derivative 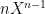 are coprime.
are coprime. 
Thus  has minimal polynomial
has minimal polynomial 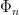 , and moreover
, and moreover  is a normal extension. We have therefore reduced our task to finding those
is a normal extension. We have therefore reduced our task to finding those  for which
for which ![{[\mathbf{Q}(\zeta_n):\mathbf{Q}] = \deg\Phi_n = \varphi(n)}](https://s0.wp.com/latex.php?latex=%7B%5B%5Cmathbf%7BQ%7D%28%5Czeta_n%29%3A%5Cmathbf%7BQ%7D%5D+%3D+%5Cdeg%5CPhi_n+%3D+%5Cvarphi%28n%29%7D&bg=ffffff&fg=000000&s=0&c=20201002) is a power of
is a power of  .
.
Writing  as a product of primes
as a product of primes 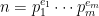 with each
with each 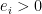 , we have (OK, the details must stop somewhere)
, we have (OK, the details must stop somewhere)

This is a power of  iff every
iff every  which occurs has
which occurs has  and
and 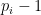 a power of
a power of  . But if
. But if 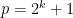 is prime, then
is prime, then 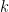 itself must be a power of
itself must be a power of  , since for every odd
, since for every odd  we have
we have
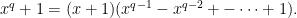
exclude
for the purpose of this post.
satisfies
for all
then
.
is immediate from the definition of
, so it suffices to prove
for each
. Fix such a
and set
. Set
. Now for a given
choose
so that
. Then
.
let
denote the largest
such that every set of
nonzero real numbers contains a subset of size
containing no solutions to
. We call such a subset sum-free.
converges as
.
be a set of size
containing no sum-free subset of size larger than
, and
a set of size
containing no sum-free subset of size larger than
. Then for large enough
, the set
is a set of size
containing no sum-free subset of size larger than
, so
. Thus by Fekete’s lemma
converges to
.
not easy to compute, but certainly
. A famously simple argument of Erdos shows
: Fix a set
, and for simplicity assume
. For
consider those
such that the fractional part of
lies between
and
. This set
is sum-free, and if
is chosen uniformly at random then
has size
on average.
, due to Malouf, shows
. The current record is due to Lewko, who showed by example
. Since these examples are somewhat ad hoc, while Erdos’s argument is beautiful, one is naturally led to the following conjecture (indeed many people have made this conjecture):
.